今天华清Java学院小编要和大家分享的是Java二叉树排序算法。排序二叉树是一种特殊的二叉树,通过这种结构可以很方便的对树中所有节点进行排序和检索。排序二叉树具有以下性质,也是实现二叉树排序所要注意的地方:
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值。
- 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值。
- 它的左,右子树也分别为排序二叉树。
简单的解释上面的几句话就是说,根节点左子树的值一定小于根节点,根节点右子树的值一定大于根节点,而根节点的左,右子树也有以上规律。排序二叉树如下图所示:
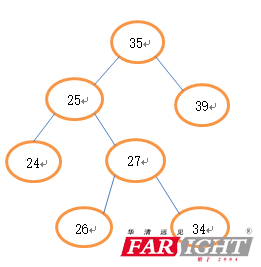
接下来分几步叙述排序二叉树的实现
Java排序二叉树实现的主体部分
由于排序二叉树是一种特殊的二叉树,所以主体部分基本和二叉树的实现差不多。
//节点类
class Node
Node parent; // 父节点
Node lChild; // 左子树
Node rChild; // 右子树
double data; // 数据
public Node(Node parent, Node lChild, Node rChild, double data) {
this.parent = parent;
this.lChild = lChild;
this.rChild = rChild;
this.data = data;
}
@Override
public String toString() {
return "[Node:" + data + "]";
}}
//排序二叉树类
public class SortedBinaryTree
private Node root; // 根节点
public SortedBinaryTree(double data) {
root = new Node(null, null, null, data);
}
// 广度遍历,也是层序遍历
public void broadTraversal() {
Queue queue = new LinkedList<>();
// 进队
queue.offer(root);
while (!queue.isEmpty()) {
//出队
Node node = (Node) queue.poll();
System.out.print(node + " ");
if (node.lChild != null) {
queue.offer(root.lChild);
}
if (node.rChild != null) {
queue.offer(root.rChild);
}}}}
Java排序二叉树的查找
这里分开介绍在上面排序二叉树类中的方法代码,写在一起显得冗长。排序二叉树查找指定节点:
// 获得指定节点
public Node getNode(double data) {
Node node = root;
while (node != null) {
if (node.data == data) {
// 等于根节点时直接返回该节点
return node;
} else if (node.data > data) {
// 左子树开始查询
node = node.lChild;
} else {
// 右子树开始查询
node = node.rChild;
}}
return null;
}
Java排序二叉树之添加节点。
插入节点运用的就是文章开头所说的性质,从根节点开始,比较数值,大于父节点添加在右边,小于则添加在左边。
//添加节点
public void add(double data){
//添加根节点
if(root==null){
root=new Node(null, null, null, data);
}else {
Node current=root;
Node parent = null;
while(current!=null)
{
parent=current;
if(current.data>data){
current=current.lChild;
}
else {
current=current.rChild;
}}
current =new Node(parent, null, null, data);
if(parent.data>current.data){
//插在左子树
parent.lChild=current;
}else {
//插在右子树
parent.rChild=current;
}}}
排序二叉树之删除节点
删除节点比较复杂,小伙伴要仔细耐心阅读以下删除情况:
1、被删除的是叶子节点,即无左、右子树,只需将它从其父节点中删除。
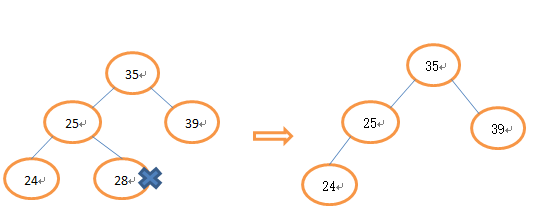
2、被删除的节点只有左(右)子树,将被删除的节点的左(右)子树补上来即可。
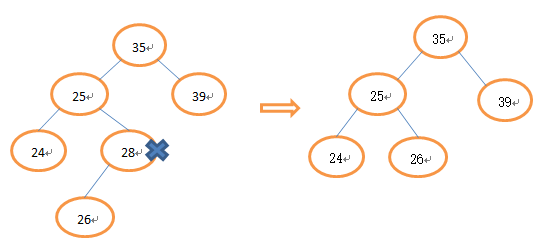
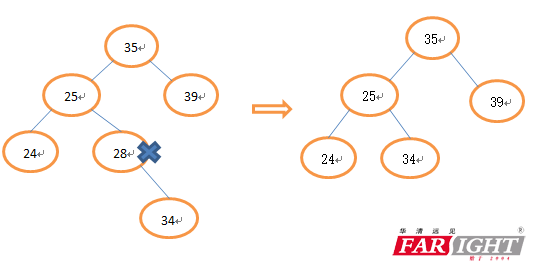
3、被删除的节点既有左子树又有右子树(这种情况比较复杂,可以有两种处理方法),选择左子树中的大节点或者选择右子树中小节点代替,即中序遍历时,被删除节点的前驱和后继节点(前驱就是中序遍历中被删除节点的前一个节点,后继就是被删除节点的后一个节点)。
(1)前驱代替被删除节点
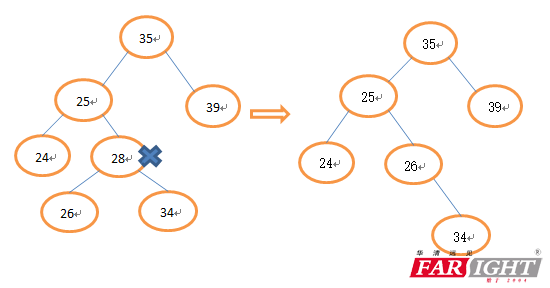
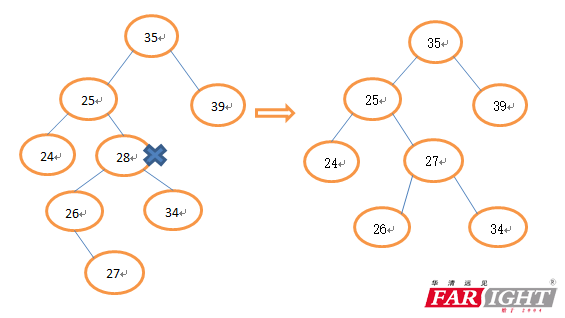
(2)后继节点代替删除节点
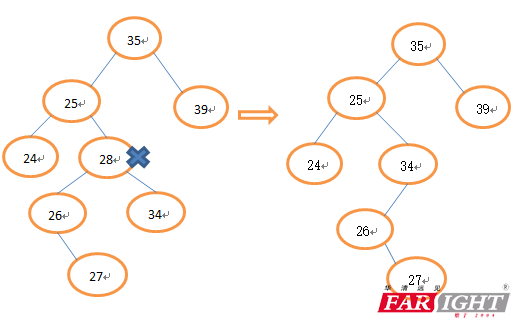
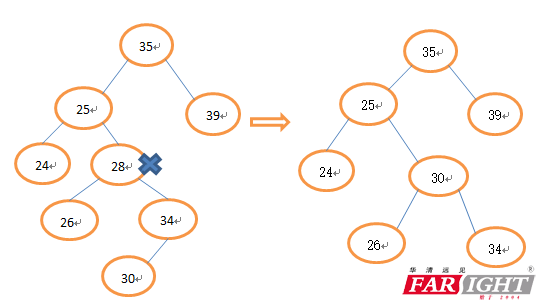
以下代码我选择了用左子树中的大节点代替被删除节点,小伙伴们也可以自己选择第二种方法来实现。
//删除指定节点
public void delete(double data) {
Node target = getNode(data);
if (target == null) {
return;
}
// 删除的节点左,右子树为空
if (target.lChild == null && target.rChild == null) {
if (target == root) {
//删除根节点
root = null;
} else {
if (target.parent.lChild == target) {
//如果target是其父节点的左孩子
target.parent.lChild = null;
} else {
//如果target是其父节点的右孩子
target.parent.rChild = null;
}
}
}
// 删除的节点左子树为空,右子树不为空
else if (target.lChild == null && target.rChild != null) {
if (target == root) {
//将根节点指向其右节点即完成删除
root = target.rChild;
} else {
if (target.parent.lChild == target) {
// 让target的父节点左子树指向target的右节点
target.parent.lChild = target.rChild;
} else {
// 让target的父节点右子树指向target的右节点
target.parent.rChild = target.rChild;
}
// 让target的父节点指向target的右孩子
target.rChild.parent = target.parent;
}
}
// 删除的节点左子树不为空,右子树为空
else if (target.lChild != null && target.rChild == null) {
if (target == root) {
root = target.lChild;
} else {
//如果target是父节点的左节点
if (target.parent.lChild == target) {
// 让target的父节点左子树指向target的左节点
target.parent.lChild = target.lChild;
} else {
// 让target的父节点右子树指向target的左节点
target.parent.rChild = target.lChild;
}
// 让target的父节点指向target的左孩子
target.lChild.parent = target.parent;
}
}
// 删除的节点左、右子树不为空
else {
Node lMaxNode = target.lChild; // 左子树上大的节点
while (lMaxNode.rChild != null) {
lMaxNode = lMaxNode.rChild;
}
//如果target左子树大节点不是target的左孩子
if(target.lChild!=lMaxNode)
lMaxNode.parent.rChild = null;
lMaxNode.parent = target.parent;
// 被删除的节点是父节点的左节点
if (target.parent.lChild == target) {
// 让target的父节点的左节点指向lMaxNode
target.parent.lChild = lMaxNode;
} else {
// 让target的父节点的右节点指向lMaxNode
target.parent.rChild = lMaxNode;
}
//如果target左子树大节点不是target的左孩子
if(lMaxNode!=target.lChild)
lMaxNode.lChild = target.lChild;
lMaxNode.rChild = target.rChild;
target.parent = null;
target.lChild = null;
target.rChild = null;
}
}
以上就完成了增删查三个操作了,由于删除操作有些复杂,建议在写代码时画图分析,以免漏掉一些情况,今天的分享就到这里了。
热点新闻












